Rettung-der-Erde.de

Die

Faszination

der

großen Zahlen

Aktualisiert: 2024-02-22

>>> zur Startseite Rettung-der-Erde.de

Themen auf dieser Seite:

X-Billionen Euro Staatsverschuldung

Wer kennt die größte Zahl?

Die Reise zum Mond mit einer Zeitung

Sonne, Mond und Sterne – die tatsächlichen Größenordnungen *)

Makrokosmos, Mikrokosmos, Nanotechnologie *)

*) Diese Artikel verwenden Zehnerpotenzen. Lesen sie ggf. vorher die Erklärung zu Zehnerpotenzen

Die Staatsverschuldung

Die Schulden des deutschen Staates belaufen sich auf über 2 Billionen Euro. Das klingt doch ganz handlich, und ich glaube, dass nicht alle, die Verantwortung dafür tragen, wirklich eine Vorstellung von der Größe dieser Zahl haben, vielleicht nicht einmal genau wissen, wie viele Nullen 1 Billion hat (nämlich 12). Im Januar 2010, als ich die nachfolgende Rechnung anstellte, waren es ca. 1,8 Billionen Euro; Legt man (theoretisch) 1,8 Billionen Euro-Stücke lückenlos nebeneinander, so ergibt sich eine Euro-Kette von 42 Millionen Kilometern Länge, die sich 1050 mal um die Erde wickeln lässt...

Stellen wir uns doch einmal vor, ein großherziger Spender würde jede Sekunde 1 Euro in einen großen Sammelbehälter werfen, um daraus die Schulden zurückzubezahlen. Wie lange würde wohl die Rückzahlung dauern? - Rein rechnerisch gut 57 000 Jahre. Aber leider wachsen die Schulden sowohl durch die Neuverschuldung als auch durch die Zinsen sehr viel schneller, so dass diese Art der Rückzahlung nur ein rapides Anwachsen der Schuldenlast nach sich ziehen würde. Allein um die Zinsen für den derzeitigen Schuldenberg zu zahlen müsste unser großherziger Münzwerfer (bei einem angenommenen Zinssatz von 3 %) pro Sekunde 1 700 Euro locker machen, während die Neuverschuldung derzeit (Januar 2010) um ca. 4 000 Euro pro Sekunde wächst!!! (die aktuellen Zahlen kann man nachlesen bei http://www.staatsverschuldung.de/schuldenuhr.htm)

Größte Zahl mit 3 Ziffern

Welches ist die größte Zahl, die man mit 3 Ziffern (ohne weitere Zeichen) darstellen kann?

999 ist es sicher nicht. 99⁹ ist ja schon nicht schlecht, und 9⁹⁹ ist noch größer; aber das ist ja noch gar nichts...

Zur Erinnerung: Was bedeutet noch dieses „hoch“? Dazu einfache Beispiele:

7 hoch 3 = 7³ = 7 mal 7 mal 7 = 343

3 hoch 7 = 3⁷ = 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 2187

Da sieht man schon, dass eine größere Hochzahl (der „Exponent“) großen Einfluss auf das Ergebnis hat.

Ein besonders einfacher und zugleich wichtiger Fall liegt vor, wenn die Grundzahl („Basis“) 10 ist. Bei solch einer Zehnerpotenz ist der Zahlenwert einfach eine 1 mit so vielen Nullen dahinter, wie die Hochzahl angibt, also beispielsweise

10 hoch 6 = 10⁶ = 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 = 1 000 000

Immer wenn man in der Wissenschaft mit sehr großen (oder sehr kleinen) Zahlen zu tun hat, schreibt man sie in Form von Zehnerpotenzen, weil diese Darstellung viel übersichtlicher ist und man dann nicht die Stellen zählen muss.

Beispiel: Die Masse der Sonne beträgt

1,989 ∙ 10³⁰ kg = 1 989 000 000 000 000 000 000 000 000 000 kg

Die linke Schreibweise kann man nach etwas Eingewöhnung viel leichter verstehen.

Nun wird man verstehen, dass es noch eine viel größere Zahl gibt, die man mit nur 3 Ziffern schreiben kann, nämlich

also 9 hoch 9 hoch 9.

Eine grobe Abschätzung lässt sich leicht machen, indem man 9 auf 10 rundet und die handlichen Zehnerpotenzen nutzt.

(Das geschwungene Gleichheitszeichen „ ≈ “ bedeutet „ist ungefähr gleich“):

also eine 1 mit 10 Milliarden Nullen dahinter. Wollten wir diese Zahl (ohne die praktische Zehnerpotenz) ausschreiben und für jede Ziffer wie üblich einen halben Zentimeter Platz berücksichtigen, beansprucht das Ergebnis eine Länge von (über)

5 Mrd. cm = 50 000 km, also mehr als den Erdumfang!

Zusatz-Information: Die drei Neunen übereinander könnte man irrtümlich auffassen als (9 hoch 9) hoch 9. Aufgrund mathematischer Vorrang-Regeln (ähnlich wie „Punkt- vor Strich-Rechnung“) bedeutet die Schreibweise ohne Klammern aber 9 hoch (9 hoch 9). Der Unterschied ist immens: So liefert die Rechnung mit der vorderen Klammer eine Zahl mit nur 88 Stellen

Eingeständnis: Die Rundung von 9 auf 10 hat ausgerechnet hier gravierende Auswirkung, weil sie im Exponenten stattfindet, wo sich jede kleine Änderung im wahrsten Sinne des Wortes potenziert. Rechnet man exakt mit 9 hoch 9 hoch 9, so wird das Ergebnis „nur“ etwa 1 848 km lang, würde aber in gedruckter Form immerhin auch noch weit über hundert richtig dicke Bücher füllen!

Denk-Aufgabe: Was ist die Hälfte von 10⁸⁰ ? >>> Lösung <<<

Mit solch großen Zahlen (wie 9 hoch 9 hoch 9) kann ein wissenschaftlicher Taschenrechner nicht rechnen. Aber es sind ja reine Zahlen-Spielereien, die hier so umwerfende Ergebnisse liefern. In den Naturwissenschaften beschäftigt man sich normalerweise mit Naturphänomenen vom Mikro-Kosmos bis zum Makro-Kosmos, und dafür reicht die

Kapazität des Rechners von 10^-99 bis 10⁹⁹ allemal.

Zur Erinnerung: „hoch minus“ bedeutet „1 durch“.

Dadurch ist 10^-99 ein winzig kleiner (positiver) Zahlenwert.

Einfachere Beispiele:

4^-1 = 1/4¹ = ¼ 4^-2 = 1/4² = ein Sechzehntel

10^-3 = 1/10³ = 1/1000 = 0,001

2,5 ∙ 10^-4 = 2,5 ∙ 1/10⁴ = 2,5 ∙ 1/10000 = 0,00025

Die Größe des Weltraumes liegt mit rund 2 ∙ 10⁸⁶ cm³ (Milli-Liter) ebenso im Rechenbereich des wissenschaftlichen Taschenrechners wie Masse des gesamten Kosmos, die "nur" etwa 10⁵⁶ Gramm beträgt, oder sein Alter, das mit ca. 13,7 Milliarden Jahren = ca. 4,32 ∙ 10¹⁷ Sekunden angegeben wird! Gehen wir in den Mikro-Kosmos, also die Welt der kleinsten Objekte, so stoßen wir auf das kleinste Atom (Wasserstoff-Atom) mit einer Masse von 1,7 ∙ 10^-27 kg, und auf den kleinsten Atom-Baustein, das Elektron, mit 9,1 ∙ 10^-31 kg, während der Durchmesser von Atomen in der Größenordnung Zehnmillionstel Millimeter (also 10^-7 mm) liegt.

Zu Beginn des 21. Jahrhunderts etablierte sich gerade die Nanotechnologie, mit deren Hilfe man Objekte oder Strukturen in der Größenordnung Nanometer *) herstellt bzw. bearbeitet, d.h. also in der Größe von etwa 10 Atomen.

*) 1 Nanometer = 10^-9 m, Nano = Milliardstel (so wie Mikro = Millionstel, und Milli = Tausendstel)

Selbst die Anzahl der Atome im Kosmos bleibt noch im Rahmen der Taschenrechner-Kapazität, da die Materie ziemlich dünn gesät ist: Im Durchschnitt muss man etwa 2 ∙ 10²⁶ m³ durchsuchen, um 1 kg zusammen zu bekommen.

Verglichen mit der Dichte von Wasser wäre das 1 Atom in 2 m³ Raum.

Hier auf der Erde findet man in 2 m³ Wasser 2 ∙ 10²⁹ Atome.

Kennen Sie dieses Rätsel?

Wir stellen uns ein ziemlich großes Blatt Zeitungspapier vor, so groß, dass man es (in Gedanken) 50 mal falten kann, also jedesmal in der Mitte knicken und doppelt übereinander legen. In Wirklichkeit schafft man es mit einem realen Blatt etwa 7 mal. Die Frage lautet nun: Wie dick würde das Teil, wenn man es wirklich 50 mal falten könnte. Etwa dicker als 1 Meter??

2 Bilder: Zuerst Zeitungsblatt einmal gefaltet, dann Zeitungsblatt 7-mal gefaltet

Zeitungsblatt einmal gefaltet Zeitungsblatt 7-mal gefaltet

Ich werde hier mal die Antwort mit der Begründung schrittweise entwickeln:

Die Dicke des Zeitungs-Papiers beträgt etwa 0,05 mm. Zweifellos wird die Dicke mit jedem Falten verdoppelt. Die Ergebnisse der einzelnen Faltungen lassen sich am leichtesten in einer Tabelle veranschaulichen:

Nach 0–mal Falten ist das Papier 0,05 mm dick.

Nach 1–mal Falten ist das Papier 0,1 mm dick.

Nach 2–mal Falten ist das Papier 0,2 mm dick.

Nach 3–mal Falten ist das Papier 0,4 mm dick.

Nach 4–mal Falten ist das Papier 0,8 mm dick.

Nach 5–mal Falten ist das Papier 1,6 mm dick.

Nach 6–mal Falten ist das Papier 3,2 mm dick.

Nach 7–mal Falten ist das Papier 6,4 mm dick.

Nach 8–mal Falten ist das Papier 12,8 mm dick.

Nach 9–mal Falten ist das Papier 25,6 mm dick.

Nach 10–mal Falten ist das Papier 51,2 mm dick.

Die ersten fünf Ergebnisse habe ich an dem abgebildeten Blatt Zeitungspapier nachgemessen und bestätigt gefunden.

Hier zeigt sich, dass durch 10-maliges Falten die ursprüngliche Dicke ungefähr vertausendfacht wurde (denn 0,05 ∙1000 = 50).

Das passiert immer, wenn man etwas zehnmal verdoppelt,

weil 2∙2∙2∙2∙2∙2∙2∙2∙2∙2 = 2¹⁰ = 1024, also ungefähr 1000 ist.

Nach der 10. Faltung haben wir noch 4 mal 10 Faltungen, also 4 mal Vertausendfachung vor uns. Viermal vertausendfachen bedeutet:

Voriges Ergebnis ∙1000∙1000∙1000∙1000.

Runden wir das vorige Ergebnis (51,2 mm) der Einfachheit halber auf 50 mm ab, so erhalten wir für die Dicke nach 50-maligem Falten

50 mm ∙ 1 000 000 000 000 = 50 000 000 000 000 mm = 50 000 000 km .

(Dabei haben wir schon zweimal während der Rechnung abgerundet!)

Mit dem 43. Falten kommen wir gerade am Mond vorbei, und beim 52. ist das obere Ende des Papierstapels schon weiter von der Erde entfernt als die Sonne!

Sonne, Mond und Sterne -- Milchstraße -- Weltall

Die Erde ist ein Nichts! Zu diesem Urteil muss jeder gelangen, der sich in einem Buch oder auf dem Bildschirm eine maßstabsgetreu verkleinerte Abbildung von Sonne und Erde ansieht, denn da ist die Erde unsichtbar (wenn sie doch zu sehen ist wie hier im oberen Bild, dann passen die Größen-Relationen nicht). Hier der Beweis:

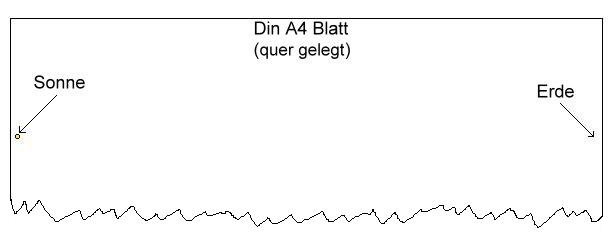
Dies ist die Abbildung von einem Din-A4-Blatt im Querformat (Original-Maße 210 mm × 297 mm, also ca. 30 cm breit). Die Entfernung von der Sonne zur Erde ist ungefähr 100 mal so groß wie der Durchmesser der Sonne. Wenn wir am linken Rand die Sonne und am rechten die Erde einzeichnen, beträgt der Abstand in der Abbildung ungefähr 30 cm, also muss die Sonne maßstabsgetreu mit einem Durchmesser von 0,01 ∙ 30 cm = 3 mm gezeichnet werden. Der Erddurchmesser beträgt nun aber wiederum etwa ein Hundertstel des Sonnendurchmessers, da bleiben für die Abbildung der Erde also 0,03 mm; deshalb ist sie unsichtbar, also ein Nichts - in Relation zu ihrer engsten Nachbarschaft im Kosmos.

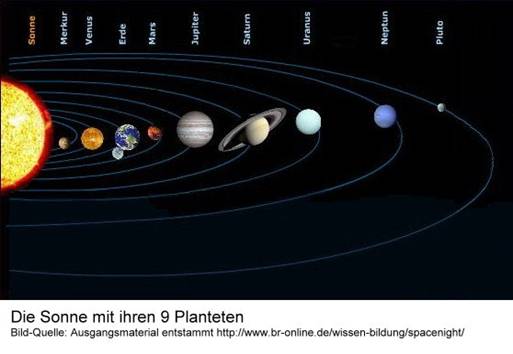
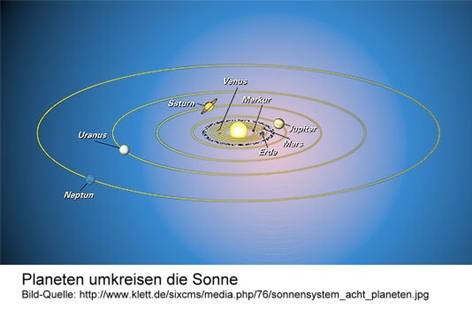
Wenn man übrigens eine maßstabsgetreue Abbildung des Sonnensystems mit allen Planeten auf ein Din-A4-Blatt zeichnen möchte, ist man schnell fertig: Man nehme ein weißes Blatt und fertig ist die Darstellung! Die Entfernung des Pluto von der Sonne ist nämlich ca. 4200 mal so groß wie der Sonnendurchmesser. Wenn wir diese Entfernung auf 30 cm verkleinern, bleibt für den Durchmesser der Sonnen-Darstellung 0,07 mm, während alle Planeten noch viel kleiner ausfallen (0,17 Tausendstel Millimeter beim Pluto). Damit ist alles unsichtbar.

Überblick: Erde - Sonne - Sonnensystem - Milchstraße – Kosmos

Die Erde umkreist mit 7 bis 8 weiteren Planeten die Sonne; das gesamte Sonnensystem mit allen seinen Planeten ist ein kleiner heller Punkt innerhalb der Milchstraße, unserer Heimat-Galaxie. Eine Galaxie ist eine große Ansammlung, ein Haufen von Sternen. Die Milchstraße beispielsweise besteht aus rund 200 Milliarden Sternen.

Abbildung der Milchstraße: Anblick von innen (linkes Bild) und von außen, „aus der Nähe“ (rechtes Bild)

Bild-Quelle: www.wikipedia.de

„Von weitem“ sieht eine Galaxie aber auch nur wie ein Stern, also ein kleiner leuchtender Punkt aus. Manche „Sterne“ (also leuchtende Punkte am Himmel) sind ganze Haufen von Galaxien… Die Ausmaße sind in der Tat galaktisch, wie die folgenden Zahlen bestätigen:

Um die Zahlenwerte in Form von Zehnerpotenzen zu verstehen, lesen Sie bitte zuerst die Erklärung zu Zehnerpotenzen
Objekt	Durchmesser
Erde	12 756 km ≈ 1,3 ∙ 10^4 km
Sonne	1 392 000 km ≈ 1,4 ∙ 10^6 km
Sonnensystem mit allen seinen Planeten	15 000 000 000 km ≈ 1,5 ∙ 10^10 km
Milchstraße (unsere Heimat-Galaxie)	10^18 km ≈ 100 000 Lichtjahre
Weltraum (Kosmos)	10^23 km ≈ 10 000 000 000 Lichtjahre
1 Lichtjahr ≈ 9,47 ∙ 10^12 km ≈ 10 Billionen km Ein Lichtjahr ist ein Längenmaß wie Meter oder Kilometer; es ist die Länge einer Strecke, für die das Licht ein Jahr benötigt, um von einem Ende zum anderen zu gelangen. Pro Sekunde bewegt sich das Licht 300 000 km weit. Wenn man diese Streckenlänge multipliziert mit 3600 (Sekunden pro Stunde) und 24 (Stunden pro Tag) und 365,25 (Tage pro Jahr), erhält man ein Lichtjahr.

Die Sonne schrumpft

Die Sonne verliert auf Grund ihrer Energie-Abstrahlung pro Sekunde 4 Millionen Tonnen Masse - und das schon seit ihrer Entstehung vor 4,6 Milliarden Jahren. Demnach hat sie schon

4,6∙10⁹∙365,25∙24∙60∙60∙4∙10⁹ kg = 5,6∙10²⁶ kg verloren.

Jahre Tage Std. Min. Sek. Masse/Sekunde

Das sind aber nur 0,03 Prozent ihrer Ausgangsmasse, die schließlich 2 ∙ 10³⁰ kg beträgt.

(Am Exponenten der Zehnerpotenz erkennt man den Faktor 10.000 in Relation zum Masse-Verlust).

>>> zurück zum Seitenanfang

Rätsel-Lösung: Die Hälfte von 10⁸⁰ ist 5 ^. 10⁷⁹

Einfacheres Beispiel: Die Hälfte von 10.000 (= 10⁴) ist 5.000 (= 5 ^. 10³)

>>> zurück

Rettung-der-Erde.de >>> zur Startseite <<<

Zwei-Liter-Auto - Generator-Elektrischer Antrieb

Geschenkte Energie: Energieversorgung - CO₂ Emission halbieren

Faszinierendes Wissen - endlich kapiert: CO2-Haushalt - Energie - Radioaktivität - große Zahlen - Strom / Spannung

Ungeschminkte Wahrheit: Fehlentwicklungen / Umweltprobleme - Wege aus der Krise

Links / Favoriten - Kontakt / Impressum